Skip to content

Commit a7fa15e

Browse files
HydrogenSulfateHydrogenSulfate
committed
update docs
1 parent 126b580 commit a7fa15e

File tree

2 files changed

+222
-1
lines changed

2 files changed

+222
-1
lines changed

‎docs/zh/examples/adv_cvit.md‎

Lines changed: 18 additions & 1 deletion
Original file line numberDiff line numberDiff line change
@@ -46,7 +46,23 @@ sciml 领域所使用的模型现阶段与CV、NLP领域的先进模型有较大
4646

4747
CVit 作为一种算子学习模型，以输入函数 $u$、函数 $s$ 的查询点 query coordinate $y$ 为输入，输出经过算子映射后的函数，在查询点 $y$ 处的函数值 $s(y)$。
4848

49-
本问题基于不连续的对流问题，求解对流方程。
49+
本问题求解如下方程：
50+
51+
Formulation The 1D advection equation in $\Omega=[0,1)$ is
52+
$$
53+
\begin{aligned}
54+
& \frac{\partial u}{\partial t}+c \frac{\partial u}{\partial x}=0 \quad x \in \Omega, \\
55+
& u(0)=u_0
56+
\end{aligned}
57+
$$
58+
where $c=1$ is the constant advection speed, and periodic boundary conditions are imposed. We are interested in the map from the initial $u_0$ to solution $u(\cdot, T)$ at $T=0.5$. The initial condition $u_0$ is assumed to be
59+
$$
60+
u_0=-1+2 \mathbb{1}\left\{\tilde{u_0} \geq 0\right\}
61+
$$
62+
where $\widetilde{u_0}$ a centered Gaussian
63+
$$
64+
\widetilde{u_0} \sim \mathbb{N}(0, \mathrm{C}) \quad \text { and } \quad \mathrm{C}=\left(-\Delta+\tau^2\right)^{-d} \text {; }
65+
$$
5066

5167
## 3. 问题求解
5268

@@ -160,3 +176,4 @@ examples/adv/adv_cvit.py
160176

161177
- [Bridging Operator Learning and Conditioned Neural Fields: A Unifying Perspective](https://arxiv.org/abs/2405.13998)
162178
- [PredictiveIntelligenceLab/cvit/adv](https://github.com/PredictiveIntelligenceLab/cvit/blob/main/adv/README.md)
179+
- [The Cost-Accuracy Trade-Off In Operator Learning With Neural Networks](https://arxiv.org/abs/2203.13181)

‎docs/zh/examples/ns_cvit.md‎

Lines changed: 204 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,204 @@
1+
# CVit(Navier-Stokes)
2+
3+
<a href="https://aistudio.baidu.com/projectdetail/8141482" class="md-button md-button--primary" style>AI Studio快速体验</a>
4+
5+
=== "模型训练命令"
6+
7+
``` sh
8+
# download data
9+
git lfs install
10+
git clone https://huggingface.co/datasets/pdearena/NavierStokes-2D
11+
python ns_cvit.py
12+
```
13+
14+
=== "模型评估命令"
15+
16+
``` sh
17+
# download data
18+
git lfs install
19+
git clone https://huggingface.co/datasets/pdearena/NavierStokes-2D
20+
python ns_cvit.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/cvit/ns_cvit_pretrained.pdparams
21+
```
22+
23+
=== "模型导出命令"
24+
25+
``` sh
26+
python ns_cvit.py mode=export
27+
```
28+
29+
=== "模型推理命令"
30+
31+
``` sh
32+
# download data
33+
git lfs install
34+
git clone https://huggingface.co/datasets/pdearena/NavierStokes-2D
35+
python ns_cvit.py mode=infer
36+
```
37+
38+
| 预训练模型 | 指标 |
39+
|:--| :--|
40+
| [ns_cvit_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/cvit/ns_cvit_pretrained.pdparams) | 4-step l2_error: 0.0398 |
41+
42+
## 1. 背景简介
43+
44+
sciml 领域所使用的模型现阶段与CV、NLP领域的先进模型有较大差别，并没有很好地利用好这些先进模型所提供的优势。因此论文作者首先提出了一个算子学习的统一视角，按照 Global conditioning 和 Local Conditioning 分别对 DeepONet、FNO、GNO 等模型进行了归纳与总结，然后基于目前广泛应用于CV、NLP领域的 Transformer 结构设计了一种 Global conditioning 的模型 CVit。相比以往的算子学习模型，参数量更小，精度更高。
45+
46+
模型结构如下图所示：
47+
48+
<img src="https://github.com/PredictiveIntelligenceLab/cvit/raw/main/figures/cvit_arch.png" alt="Cvit" width="800">
49+
50+
## 2. 问题定义
51+
52+
CVit 作为一种算子学习模型，以输入函数 $u$、函数 $s$ 的查询点 query coordinate $y$ 为输入，输出经过算子映射后的函数，在查询点 $y$ 处的函数值 $s(y)$。
53+
54+
本问题基于固定方腔的不可压 buoyancy-driven flow 即方腔内的浮力驱动流动问题，求解如下方程：
55+
56+
Formulation We consider the vorticity-stream $(\omega-\psi)$ formulation of the incompressible Navier-Stokes equations on a two-dimensional periodic domain, $D=D_u=D_v=[0,2 \pi]^2$ :
57+
$$
58+
\begin{aligned}
59+
& \frac{\partial \omega}{\partial t}+(v \cdot \nabla) \omega-v \Delta \omega=f^{\prime} \\
60+
& \omega=-\Delta \psi \quad \int_D \psi=0, \\
61+
& v=\left(\frac{\partial \psi}{\partial x_2},-\frac{\partial \psi}{\partial x_1}\right)
62+
\end{aligned}
63+
$$
64+
65+
## 3. 问题求解
66+
67+
接下来开始讲解如何将问题一步一步地转化为 PaddleScience 代码，用深度学习的方法求解该问题。
68+
为了快速理解 PaddleScience，接下来仅对模型构建、方程构建、计算域构建等关键步骤进行阐述，而其余细节请参考 [API文档](../api/arch.md)。
69+
70+
### 3.1 模型构建
71+
72+
在本问题中，对于每一个函数 $u$，其经过算子学习模型映射到 $s$ 后，在 $y$ 上都有对应的标签 $s(y)$，因此在这里使用 CVit 来表示 $(u, y)$ 到 $s(y)$ 的映射关系：
73+
74+
$$
75+
s(y) = G(u)(y)
76+
$$
77+
78+
上式中 $G(u)$ 即为 CVit 模型本身，用 PaddleScience 代码表示如下
79+
80+
``` py linenums="80"
81+
--8<--
82+
examples/ns/ns_cvit.py:80:81
83+
--8<--
84+
```
85+
86+
为了在计算时，准确快速地访问具体变量的值，在这里指定网络模型的输入变量名是 `("u", "y")`，输出变量名是 `("s")`，这些命名与后续代码保持一致。
87+
88+
接着通过指定 CVit 的输入维度、坐标维度、输出维度、模型层数等超参数，就可实例化出了一个 `model`
89+
90+
``` yaml linenums="40"
91+
--8<--
92+
examples/ns/conf/ns_cvit_small_8x8.yaml:40:59
93+
--8<--
94+
```
95+
96+
### 3.2 数据准备
97+
98+
本问题中的数据分片储存在 `NavierStokes2D/*.h5` 文件中，分为训练和测试集，其数据包含内容如下表所示（这些信息会在运行时打印出来）。
99+
100+
| 文件名 | 文件数量 | 数据形状 | 输入形状 | 标签形状 |
101+
| :-- | :-- | :-- | :-- | :-- |
102+
| NavierStokes2D_train_*.h5 | 52 |`[1000, 14, 128, 128, 3]` | `[4000, 10, 128, 128, 3]` | `[4000, 1, 128, 128, 3]` |
103+
| NavierStokes2D_test_*.h5 | 41 | `[5200, 14, 128, 128, 3]` | `[20800, 10, 128, 128, 3]` | `[20800, 1, 128, 128, 3]` |
104+
105+
数据读取函数如下：
106+
107+
``` py linenums="27"
108+
--8<--
109+
examples/ns/ns_cvit.py:27:76
110+
--8<--
111+
```
112+
113+
训练、测试时采用前 10 个时刻预测下一个时刻，并且测试时会以自回归的形式连续预测 4 个时刻。
114+
115+
### 3.3 约束构建
116+
117+
#### 3.3.1 监督约束
118+
119+
在训练时，随机选取 `batch_size` 组来自 $u$ 上的数据、并同时随机选取 `query_point` 个 $y$ 坐标，如此构成了训练输入数据，标签数据则从 $s$ 中随机选取同样的 `batch_size` x `query_point` 个标签点。
120+
121+
``` py linenums="104"
122+
--8<--
123+
examples/ns/ns_cvit.py:104:145
124+
--8<--
125+
```
126+
127+
`SupervisedConstraint` 的第一个参数是用于训练的数据配置，我们使用 `NamedArrayDataset` 作为数据集类型，并且传入自定义的`random_query`作为`transforms`，完成上述的样本随机选取过程；
128+
129+
第二个参数是该约束的计算表达式，我们只需要计算 $s$ 即可，因此填入一个不做任何处理，直接取出模型输出结果"s"的匿名表达式；
130+
131+
第三个参数是损失函数，此处选用 `MSELoss` 函数；
132+
133+
第四个参数是约束条件的名字，需要给每一个约束条件命名，方便后续对其索引。此处命名为 "Sup" 即可。
134+
135+
### 3.4 超参数设定
136+
137+
接下来需要指定训练轮数和学习率，此处按实验经验，使用 200 轮训练轮数，初始学习率为 0.001，预热轮数为 5，全局梯度裁剪系数为 1.0，权重衰减为 1e-5。
138+
139+
``` yaml linenums="61"
140+
--8<--
141+
examples/ns/conf/ns_cvit_small_8x8.yaml:61:79
142+
--8<--
143+
```
144+
145+
### 3.5 优化器构建
146+
147+
训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器，并配合使用机器学习中常用的 ExponentialDecay 学习率调整策略。
148+
149+
``` py linenums="147"
150+
--8<--
151+
examples/ns/ns_cvit.py:147:155
152+
--8<--
153+
```
154+
155+
### 3.6 评估器构建
156+
157+
在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 `ppsci.validate.SupervisedValidator` 构建评估器。
158+
159+
``` py linenums="157"
160+
--8<--
161+
examples/ns/ns_cvit.py:157:202
162+
--8<--
163+
```
164+
165+
过程中我们使用了自定义的评估函数 `l2_err_func`，用于评估测试集上所有样本、三个输出物理量的 2-范数误差。
166+
167+
### 3.7 模型训练、评估
168+
169+
完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估。
170+
171+
``` py linenums="204"
172+
--8<--
173+
examples/ns/ns_cvit.py:204:213
174+
--8<--
175+
```
176+
177+
## 4. 完整代码
178+
179+
``` py linenums="1" title="ns_cvit.py"
180+
--8<--
181+
examples/ns/ns_cvit.py
182+
--8<--
183+
```
184+
185+
## 5. 结果展示
186+
187+
在测试集上的预测结果、参考结果以及绝对值误差如下图所示。
188+
189+
<figure markdown>
190+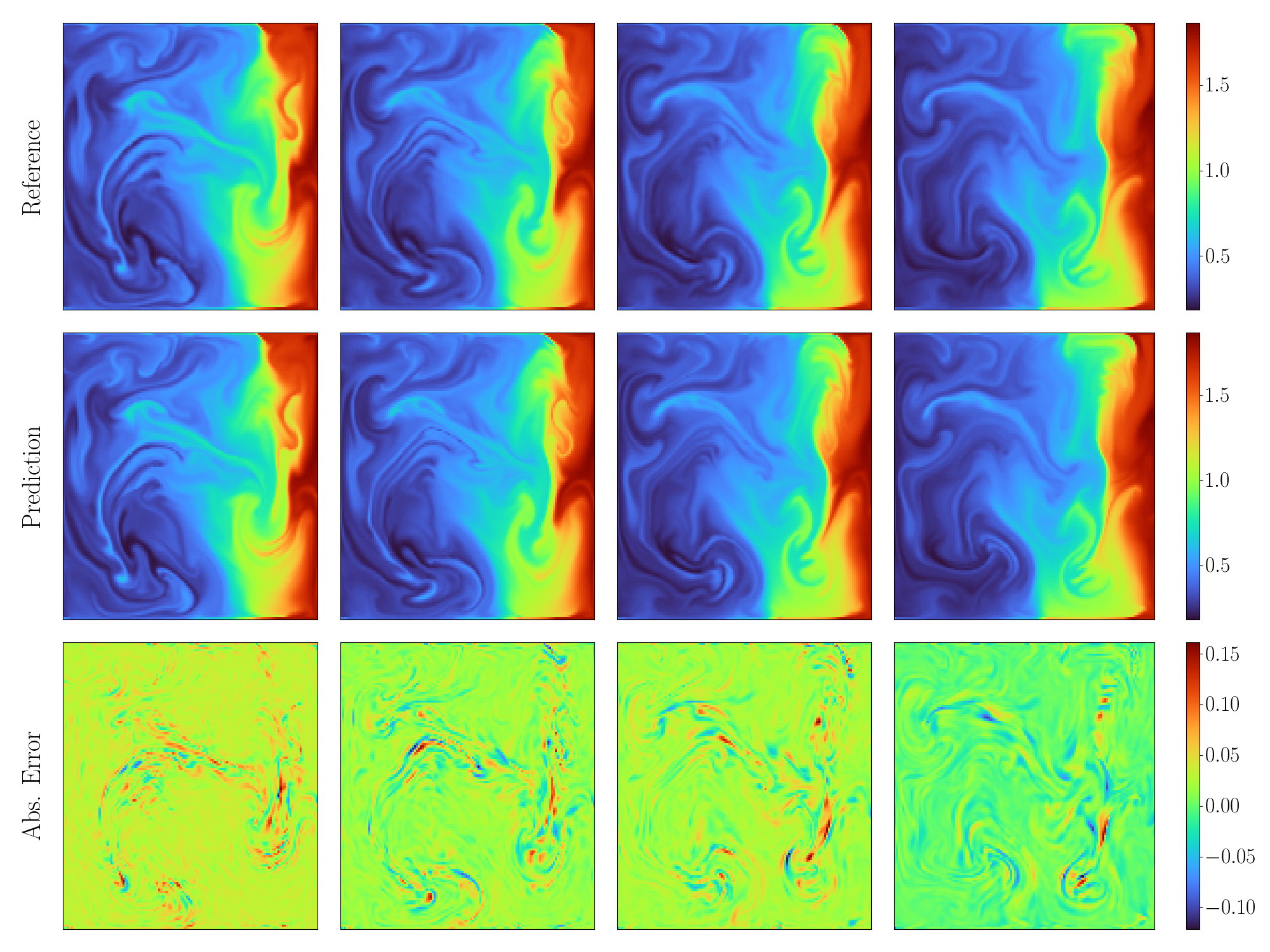
![ns_u.jpg](https://paddle-org.bj.bcebos.com/paddlescience/docs/cvit/ns_u.png){ loading=lazy }
191+
<figcaption> 左侧为 CVit 对物理量 u 的预测结果，中间为物理量 u 的参考结果，右侧为两者的差值</figcaption>
192+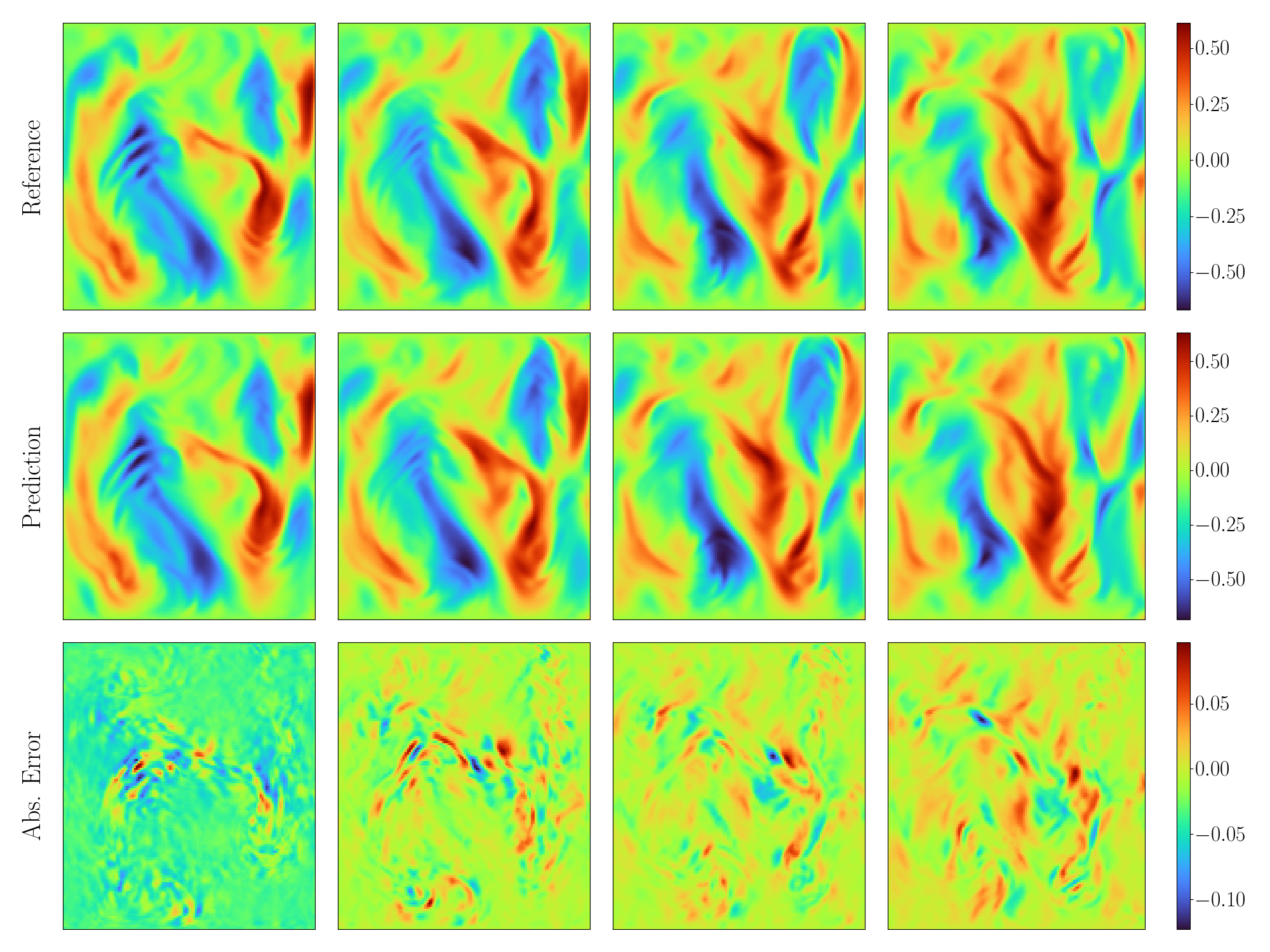
![ns_ux.jpg](https://paddle-org.bj.bcebos.com/paddlescience/docs/cvit/ns_ux.png){ loading=lazy }
193+
<figcaption> 左侧为 CVit 对物理量 ux 的预测结果，中间为物理量 ux 的参考结果，右侧为两者的差值</figcaption>
194+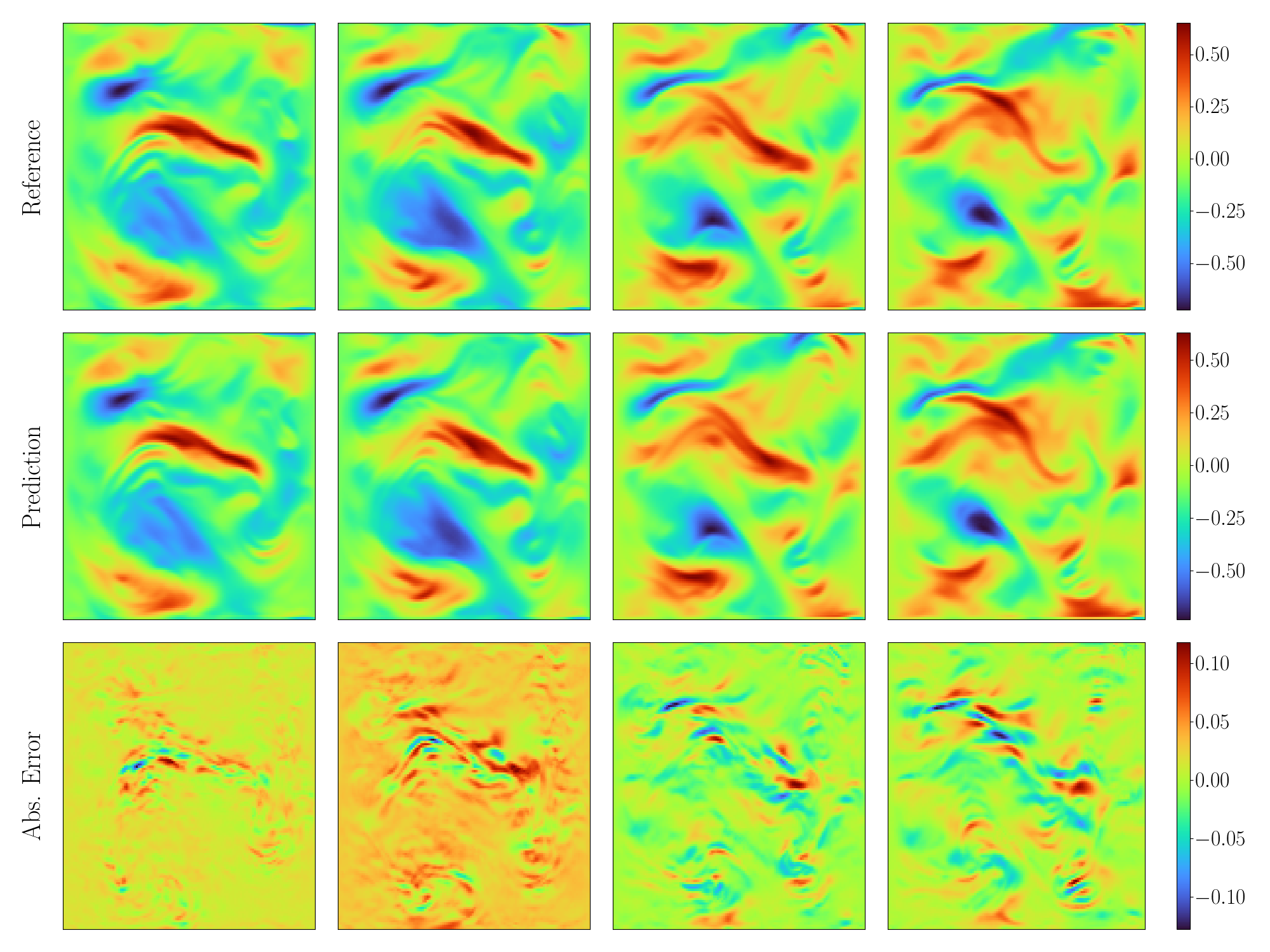
![ns_uy.jpg](https://paddle-org.bj.bcebos.com/paddlescience/docs/cvit/ns_uy.png){ loading=lazy }
195+
<figcaption> 左侧为 CVit 对物理量 uy 的预测结果，中间为物理量 uy 的参考结果，右侧为两者的差值</figcaption>
196+
</figure>
197+
198+
可以看到模型的三个预测物理量和参考结果基本一致，通过自回归的方式，连续推理 4 步的平均误差为 0.039%。
199+
200+
## 6. 参考资料
201+
202+
- [Bridging Operator Learning and Conditioned Neural Fields: A Unifying Perspective](https://arxiv.org/abs/2405.13998)
203+
- [PredictiveIntelligenceLab/cvit/ns](https://github.com/PredictiveIntelligenceLab/cvit/blob/main/ns/README.md)
204+
- [The Cost-Accuracy Trade-Off In Operator Learning With Neural Networks](https://arxiv.org/abs/2203.13181)

0 commit comments

Comments
 (0)