diff --git a/docs/source/ko/_toctree.yml b/docs/source/ko/_toctree.yml
index 80bd4c991a5b..eed3877c95f7 100644
--- a/docs/source/ko/_toctree.yml
+++ b/docs/source/ko/_toctree.yml
@@ -174,8 +174,8 @@
     title: BERTology
   - local: in_translation
     title: (번역중) Perplexity of fixed-length models
-  - local: in_translation
-    title: (번역중) Pipelines for webserver inference
+  - local: perplexity
+    title: 고정 길이 모델의 펄플렉서티(Perplexity)
   title: (번역중) 개념 가이드
 - sections:
   - sections:
diff --git a/docs/source/ko/perplexity.md b/docs/source/ko/perplexity.md
new file mode 100644
index 000000000000..72eee0643c33
--- /dev/null
+++ b/docs/source/ko/perplexity.md
@@ -0,0 +1,135 @@
+<!--Copyright 2020 The HuggingFace Team. All rights reserved.
+
+Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with
+the License. You may obtain a copy of the License at
+
+http://www.apache.org/licenses/LICENSE-2.0
+
+Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on
+an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the
+specific language governing permissions and limitations under the License.
+-->
+
+# 고정 길이 모델의 펄플렉서티(Perplexity)[[perplexity-of-fixedlength-models]]
+
+[[open-in-colab]]
+
+펄플렉서티(Perplexity, PPL)는 가장 일반적인 언어 모델 평가지표 중 하나입니다.
+자세히 알아보기 전에 이 평가지표는 고전적인 언어 모델(자기회귀 또는 인과적 언어 모델이라고도 함)에만 적용되며 BERT와 같은 마스킹된 언어 모델에는 잘 적용하지 않습니다 (BERT는 [summary of the models](../en/model_summary) 문서를 참고하세요).
+
+펄플렉서티는 시퀀스의 음의 로그 우도(negative log-likelihood, NLL) 값의 평균에 지수(exponentiate)를 취한 값으로 정의됩니다.
+토큰화된 시퀀스 \\(X = (x_0, x_1, \dots, x_t)\\) 가 있을 때, \\(X\\) 의 펄플렉서티는 아래 수식과 같이 구할 수 있습니다.
+
+$$\text{PPL}(X) = \exp \left\{ {-\frac{1}{t}\sum_i^t \log p_\theta (x_i|x_{<i}) } \right\}$$
+
+\\(\log p_\theta (x_i|x_{<i})\\) 는 모델에 i번째 이전까지 토큰이 주어졌을 때 i번째 토큰의 로그 우도값입니다.
+
+직관적으로 말뭉치에서 지정된 토큰 집합을 균일하게 예측하는 모델의 능력에 대한 평가로 생각할 수 있습니다.
+중요한 점은 토큰화 과정이 모델의 펄플렉서티에 직접적인 영향을 미치므로 서로 다른 모델을 비교할 때 항상 이를 고려해야 합니다.
+
+이는 데이터와 모델 예측 간의 cross-entropy 값에 지수를 취한 것과 동일합니다.
+펄플렉서티와 문자당 비트 수(BPC) 및 데이터 압축과의 관계에 대해 더 직관적인 이해를 원하신다면 다음 글
+[fantastic blog post on The Gradient](https://thegradient.pub/understanding-evaluation-metrics-for-language-models/)을 확인하세요.
+
+## 고정 길이 모델의 펄플렉서티(PPL) 계산하기[[calculating-ppl-with-fixedlength-models]]
+
+모델의 컨텍스트 크기가 정해져있지 않다면,
+아래와 같이 시퀀스를 자동 회귀적으로 분해하고 각 단계에서 선행 하는 전체 시퀀스를 조건부 확률에 넣어 모델의 펄플렉서티를 계산할 것입니다.
+
+<img width="600" alt="Full decomposition of a sequence with unlimited context length" src="https://huggingface.co/datasets/huggingface/documentation-images/resolve/main/ppl_full.gif"/>
+
+그러나 모델의 근사치를 구할 때는 일반적으로 모델이 처리할 수 있는 토큰 수에 제한이 있습니다.
+예를 들어, 가장 큰 버전의 [GPT-2](model_doc/gpt2)는 토큰의 길이가 1024로 고정되어 있습니다.
+따라서 \\(t\\) 가 1024보다 큰 경우에 \\(p_\theta(x_t|x_{<t})\\) 을 계산할 수 없습니다.
+
+대신 시퀀스는 일반적으로 모델의 최대 입력 크기와 동일한 길이는 가지는 부분 시퀀스로 쪼갭니다.
+만약 모델의 최대 입력 길이가 \\(k\\) 라면, 
+토큰 \\(x_t\\) 의 우도 값을 계산할 때 이전 토큰을 모두 사용하지 않고, \\(k-1\\) 토큰까지 사용해 대략적인 우도 값을 추정합니다. 
+
+모델의 시퀀스에 대한 펄플렉서티를 계산할 때,
+수월하지만 차선책은 시퀀스를 청크로 쪼개고 분해된 각 부분의 로그 우도 값을 독립적으로 합산하는 것입니다.
+
+<img width="600" alt="Suboptimal PPL not taking advantage of full available context" src="https://huggingface.co/datasets/huggingface/documentation-images/resolve/main/ppl_chunked.gif"/>
+
+이 방법은 각 부분의 펄플렉서티를 한 번의 포워드 패스로 계산할 수 있어 빠르지만 일반적으로 더 높은(더 나쁜) PPL을 산출합니다.
+왜냐하면 대부분의 예측 단계에서 모델의 컨텍스트가 적기 때문입니다.
+
+대신, 고정 길이 모델의 PPL은 슬라이딩 윈도우 전략으로 평가해야 합니다.
+이 전략에는 컨텍스트 윈도우을 반복적으로 슬라이딩해 모델이 각 예측을 수행할 때 더 많은 컨텍스트를 갖도록 하는 작업이 포함됩니다.
+
+<img width="600" alt="Sliding window PPL taking advantage of all available context" src="https://huggingface.co/datasets/huggingface/documentation-images/resolve/main/ppl_sliding.gif"/>
+
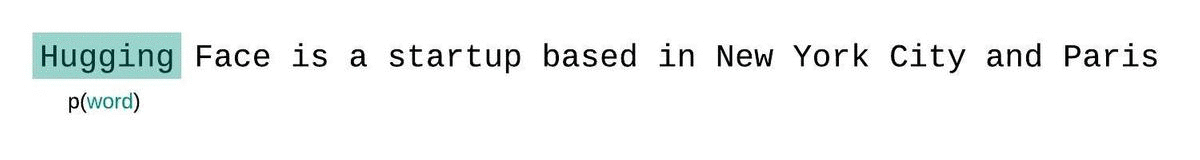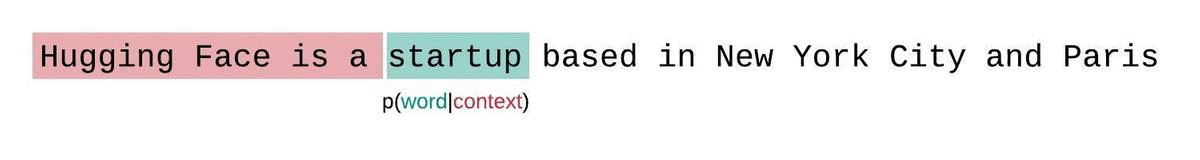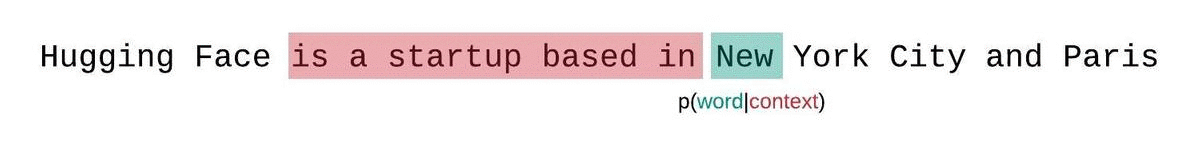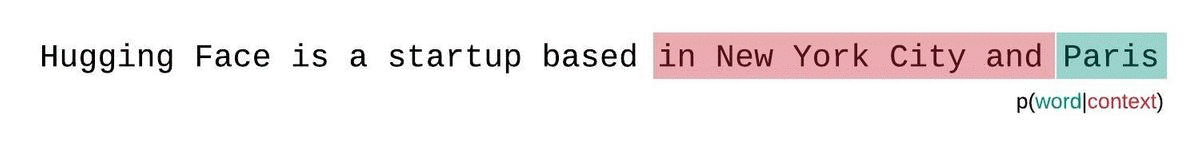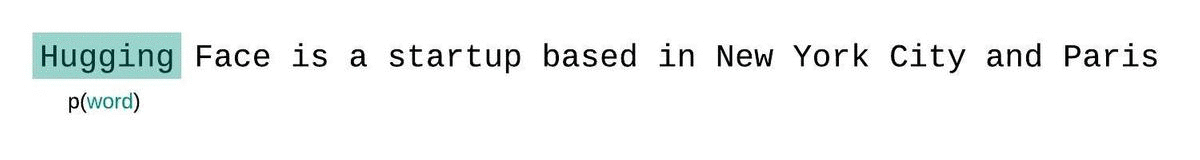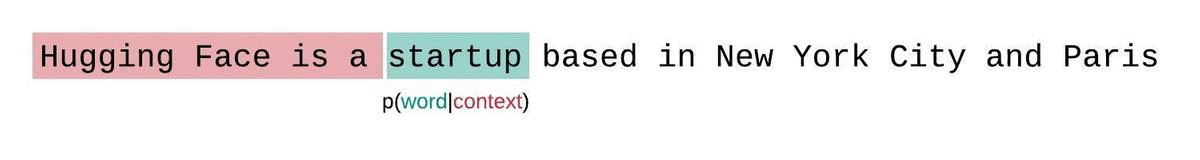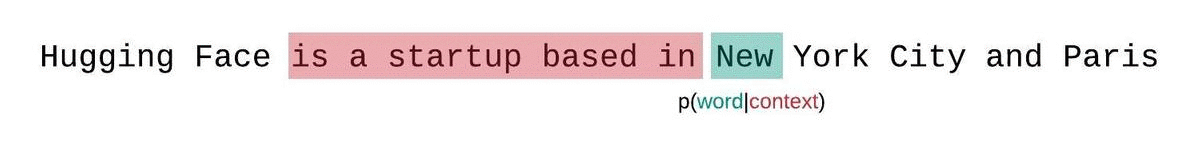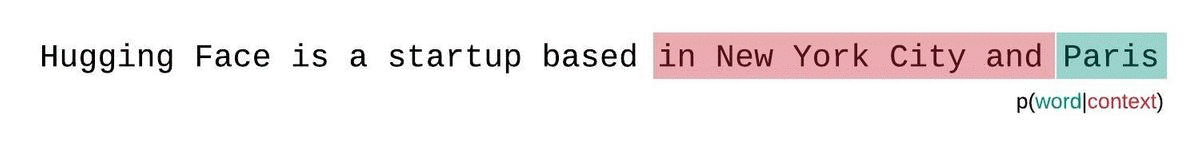+이는 시퀀스 확률의 실제 분해에 더 가까운 근사치이며 일반적으로 더 유리한 점수를 산출합니다.
+단점은 말뭉치의 각 토큰에 대해 별도의 포워드 패스가 필요하다는 것입니다.
+현실적으로 좋은 절충안은 한 번에 한 토큰씩 슬라이딩하는 것이 아니라 더 큰 간격으로 컨텍스트를 이동하는 스트라이드가 적용된 슬라이딩 윈도우을 사용하는 것입니다. 
+이렇게 하면 계산을 훨씬 더 빠르게 진행하면서도 모델에 각 단계에서 예측을 수행할 수 있는 긴 컨텍스트를 제공할 수 있습니다.
+
+## 예제: 🤗 Transformers에서 GPT-2로 펄플렉서티(perplexity) 계산하기[[example-calculating-perplexity-with-gpt2-in-transformers]]
+
+이제 GPT-2로 위의 과정을 시연해 보겠습니다.
+
+```python
+from transformers import GPT2LMHeadModel, GPT2TokenizerFast
+
+device = "cuda"
+model_id = "gpt2-large"
+model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
+tokenizer = GPT2TokenizerFast.from_pretrained(model_id)
+```
+
+WikiText-2 데이터 세트를 가져오고 몇 가지 슬라이딩 윈도우 전략을 사용해 펄플렉서티를 계산해보겠습니다.
+이 데이터 세트는 크기가 작고 포워드 패스 한 번만 수행하기 때문에 전체 데이터 세트를 메모리에 가져오고 인코딩할 수 있습니다.
+
+```python
+from datasets import load_dataset
+
+test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
+encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")
+```
+
+🤗 Transformers를 사용하면 모델의 `labels`로 `input_ids`를 전달해 각 토큰에 대한 평균 음의 우도 값을 손실로 반환할 수 있습니다.
+하지만 슬라이딩 윈도우 방식을 사용하면 각 반복마다 모델에 전달하는 토큰이 겹칩니다.
+컨텍스트로 처리하는 토큰에 대한 로그 우도 값이 손실에 포함되는 것을 원하지 않기 때문에 이러한 토큰의 `input_ids`를 `-100`으로 설정하여 무시할 수 있습니다. 
+
+다음은 스트라이드(stride)를 `512`로 사용한 예시입니다. 
+즉, 모델이 한 토큰의 조건부 우도 값을 계산할 때 컨텍스트에 최소한 512개의 토큰이 포함되어있다는 의미입니다 (해당 토큰 앞에 512개의 토큰이 있는 경우).
+
+```python
+import torch
+from tqdm import tqdm
+
+max_length = model.config.n_positions
+stride = 512
+seq_len = encodings.input_ids.size(1)
+
+nlls = []
+prev_end_loc = 0
+for begin_loc in tqdm(range(0, seq_len, stride)):
+    end_loc = min(begin_loc + max_length, seq_len)
+    trg_len = end_loc - prev_end_loc  # 마지막 루프의 스트라이드 값과 다를 수 있음
+    input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
+    target_ids = input_ids.clone()
+    target_ids[:, :-trg_len] = -100
+
+    with torch.no_grad():
+        outputs = model(input_ids, labels=target_ids)
+
+        # 손실은 모든 유효한 레이블에 대한 평균값을 구하는 교차 엔트로피(cross entropy)로 계산됩니다.
+        # 나이브 베이지안 모델은 내부적으로 레이블을 왼쪽으로 1개씩 밀기 때문에, (타켓 - 1)개 만큼의 레이블에 대해 손실을 계산합니다.
+        neg_log_likelihood = outputs.loss
+
+    nlls.append(neg_log_likelihood)
+
+    prev_end_loc = end_loc
+    if end_loc == seq_len:
+        break
+
+ppl = torch.exp(torch.stack(nlls).mean())
+```
+
+스트라이드를 최대 입력 길이와 동일하게 설정하면 위에서 설명한 차선책인 비슬라이딩 윈도우 전략과 동일합니다.
+일반적으로 스트라이드가 작을수록 모델이 각 예측을 할 때 더 많은 컨텍스트를 볼 수 있게 되어 펄플렉서티 값이 좋아집니다.
+
+위의 계산을 토큰이 겹치지 않도록 `stride = 1024`로 설정하면 PPL은 `19.44`로 GPT-2 논문에서 보고된 `19.93`과 거의 동일합니다.
+`stride = 512`로 슬라이딩 윈도우 전략을 사용하면 PPL은 `16.45`로 떨어집니다. 
+이는 더 좋은 점수일 뿐만 아니라 시퀀스 확률의 실제 자동 회귀 분해에 더 가까운 방식으로 계산됩니다.
\ No newline at end of file