-
Notifications
You must be signed in to change notification settings - Fork 2
Ungapped Alignment Phase
Once BLAST collects seed hits, the next phase is to convert a subset of these hits into ungapped alignments. Before the capability for gapped alignments was added, the majority of the work BLAST performs fell into this phase. The actual code has many more twists and turns than its description in the 1997 BLAST paper would indicate. The BLAST-program-specific subsystem that creates ungapped alignments is called the wordfinder for that BLAST program.
It will be very helpful to visualize an ungapped alignment between a query sequence Q and a subject sequence S graphically. To that end, create a table with letters of Q labeling the rows and letters of S labeling the columns:
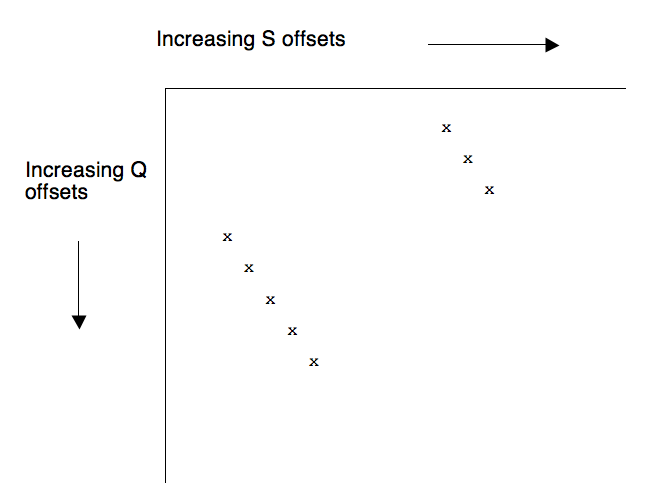
In the "dot plot" above, ungapped alignments between Q and S are represented as diagonal strings of x's. Such alignments are also called high-scoring pairs or high-scoring segment pairs (both are abbreviated 'HSP'). The job of the wordfinder is to produce all of the HSPs between Q and S whose alignment score exceeds a cutoff value.
Any line in the dot plot where S[i] - Q[i] = c for all i is referred to as diagonal c. Diagonals extend from the top left of the plot to the bottom right. An ungapped alignment occurs on exactly one diagonal, and several ungapped alignments can share the same diagonal.
The input to all of the wordfinders is a stream of BlastOffsetPair structures from one of the various ScanSubject routines. The simplest protein ungapped wordfinder (not the default) is described in BlastAaWordFinder_OneHit and is called from the top-level routine BlastAaWordFinder (in aa_ungapped.c).
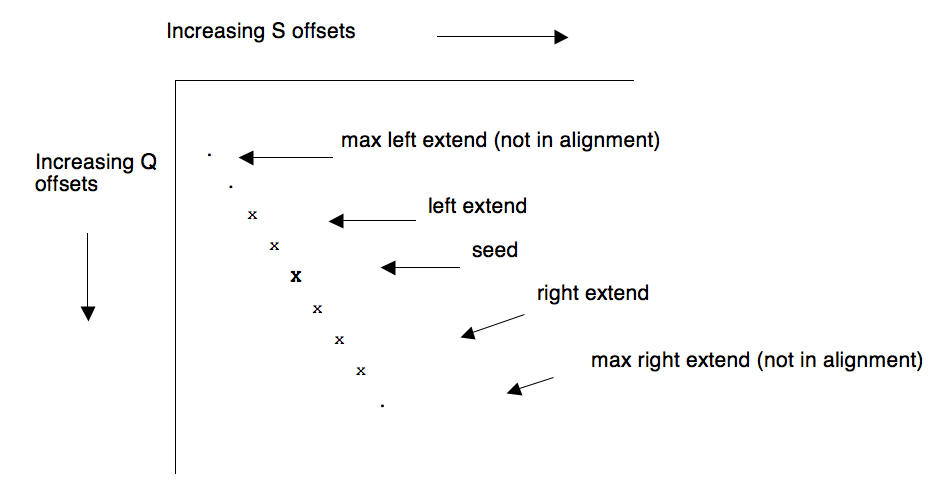
Each BlastOffsetPair gives the offsets into Q and S where a seed ungapped alignment (typically three letters long for protein searches) begins. For each such offset pair, BlastAaWordFinder_OneHit attempts to extend the seed alignment to the left and the right by some distance. The extension process uses an 'X-drop' algorithm: starting from the score of the seed, the running score of the alignment is kept. For extensions in one direction, if aligning the next letter of Q and S increases the running score above its previous best value, the alignment is enlarged to include that letter pair. If adding the next letter reduces the total alignment score by more than some constant X (an input to the algorithm) below the current best alignment score, the extension stops. If neither of these happens, extension continues but the alignment is not enlarged. The assumption is that once the running score dips below the X-drop threshold, it will never improve the alignment again. The larger X is, the longer the algorithm works before giving up.
More formally, the steps involved are as follows (see BlastAaExtendOneHit in aa_ungapped.c):
-
Given the initial seed hit, find the highest scoring subregion inside the seed. This process by itself is a tiny (the length of the seed) ungapped extension. The subregion so produced has 1, 2, or 3 contiguous letters for word size 3.
-
Set the running score to the score of the above subregion. Starting with the first letter pair to the left of the subregion, run the X-drop algorithm to extend to the left. Remember the maximum score encounterd and the offset of that maximum score.
-
Set the running score to the maximum from step 2. Starting with the first letter pair to the right of the subregion, run the X-drop algorithm to extend to the right. This time, extension stops if the X-drop test fails or if the running score ever drops to 0 or below. Remember the maximum score encountered and the offset of that maximum score.
Either or both of steps 2 and 3 can fail immediately, i.e. the extension fails on the first letter pair outside the region found in step 1. Step 1 is extremely important: if the left-hand letters of the seed are low-scoring, step 1 guarantees that the X-drop test will fail as soon as possible, while leaving a locally high running score to help the right extension in step 3.
The extra terminating condition in step 3 is a bit subtle. The left extension keeps going until the X-drop test fails, so the offset to the left really is the left endpoint of an optimal alignment. If the extension to the right reaches a running score of zero, but the optimal right-hand endpoint was beyond this, then you could have thrown away all of the alignment that lies to the left of the zero point (because the alignment left of the zero point would make no net contribution to the alignment right of the zero point). Left of the zero point could still be optimal, but the above shows that an optimal alignment will not include a zero point, and so step 3 lets you quit early (i.e. possibly before the X-drop test would actually have failed).
There is a fairly complicated asymmetry here. Extending left will give an optimal alignment that may or may not include the seed (if the score threshold T >= X and step 1 is performed then the seed is included in the left extension). If this extension turns out to be too long and a higher-scoring but shorter alignment is possible, later seeds that start farther to the right on the same diagonal will find that better alignment. However, extending too far to the right could prevent the wordfinder from ever considering the current portion of the diagonal again because of the optimization described next.
Once the range and the score of the ungapped extension is computed, if the score exceeds a cutoff value then the details of the extension are saved in a BlastInitHSP structure (BLAST_extend.h). The complete collection of ungapped alignments is kept in a BlastInitHitlist structure that is passed on for subsequent processing when all such ungapped alignments have been computed.
Even small ungapped alignments may contain clusters of seeds. For the BLOSUM62 score matrix, the following ungapped alignment:
Query: 6 ALWDYEPQNDDELPMKEGDCMTI 28
AL+DY+ + ++++ + GD +T+
Sbjct: 6 ALYDYKKEREEDIDLHLGDILTV 28
contains 4 triplets of letters whose combined score is 11 or more. If the extension procedure described above is performed on all 4 seeds, most likely all four extensions would produce the same ungapped alignment. This is wasteful, since three of the alignments would have to be thrown away later. To remove the potential for duplicate extensions when seeds are packed close together, a method is needed to remember when a previous alignment has already covered the neighborhood of Q and S that a given seed would explore if it was extended.
In general, when an ungapped extension happens, the region of Q and S that is explored will exceed the size of the final alignment:
Since the entire extension uses the same diagonal, we can remember the largest 'distance' to the right that is traversed on this diagonal by this alignment, and if future seeds wind up on the same diagonal at a distance less than this number then we know they can be immediately discarded. Further, if seeds only occur on diagonals in order of increasing distance, then we don't have to store the maximum extent explored by each alignment, only the maximum extent of the last alignment to hit this particular diagonal. In other words, last-hit information can occur on a per-diagonal rather than per-hit basis.
In a dot plot for Q and S, the number of distinct diagonals is (size of Q) + (size of S) - 1. However, if the list of (Q,S) offsets has the offsets into S arranged in ascending order (the ScanSubject routines work this way), then dealing with the distinct subject offsets is equivalent to sweeping a vertical line from left to right across the dot plot. When the vertical line moves to the right by one position, one diagonal becomes invalid (at the bottom of the plot) and another diagonal becomes active (at the top of the plot):
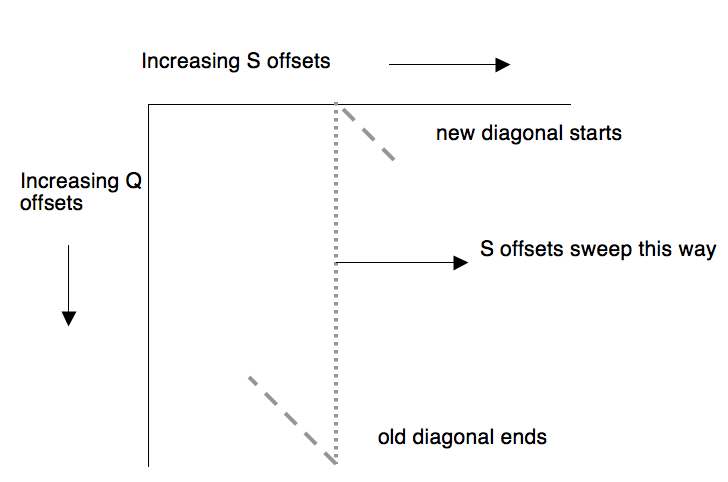
Hence the total number of diagonals active at one time is (size of Q).
Diagonal distance is tracked by an array of type DiagStruct. Given offset q_off into Q and offset s_off into S, the diagonal information for the pair is at offset (s_off - q_off) mod (size of Q) in the array. Within this entry, the DiagStruct::last_hit field contains the maximum subject offset of the last hit to this diagonal. If this number exceeds s_off then no ungapped extension is necessary. However, if s_off is larger, then an ungapped extension is performed with seed (q_off, s_off). The only difference is that the extension to the right saves the maximum S offset that was examined. Whether or not the resulting ungapped alignment scores high enough to be saved, last_hit is set to (max offset examined - (wordsize-1)). Any future seeds that lie on this diagonal, and whose subject offsets exceed this number, have at least one letter in the seed lying beyond the extent of the previous alignment on this diagonal.
A nice property of this method is that if the computation of diagonal entry puts the current seed on a diagonal that was just invalidated, the value of last_hit there is at most s_off-1 (because offset s_off is currently being processed). s_off will always exceed this number, so the ungapped extension will always be performed. This allows invalid diagonal structures to automatically be recycled for use by new diagonals.
One easy way to reduce the overhead of using diagonals is to make the total number of DiagStruct entries a power of two. More specifically, the number of entries should be the smallest power of two exceeding the size of the query sequence. This way, calculating the offset into the diag array only involves a mask operation rather than a full integer remainder.
Use of the diag array further requires that all last_hit fields be initialized to zero for each subject sequence. When the query is large (i.e. the diag array is large) and the database contains many small sequences, the overhead of clearing the diag array becomes significant.
A trick allows avoiding this overhead almost all the time. When the last_hit field is updated, a bias is added to the new value. The bias is subtracted from last_hit before the comparison to s_off is made to determine whether an ungapped extension is needed. After the entire subject sequence has been processed, Blast_ExtendWordExit adds the length of the subject sequence to the bias. When the next sequence is being processed, the bias is larger than any of the leftover last_hit entries in the diag array, and so subtracting it from any last_hit will make new subject offsets automatically larger than all of the leftover last_hit entries from the previous sequence. In this way the recycling of diag entries happens not only within a subject sequence but also between different subject sequences. Clearing of the diag array is only necessary when the bias value threatens to cause integer overflow; when the bias exceeds 230, Blast_ExtendWordExit explicitly clears the diag array and sets the bias to zero.
All of the information concerning the diag array is packed into a BLAST_DiagTable structure (BLAST_extend.h). This includes the diag entries themselves, the array size, the mask for locating diagonals, and the bias (BLAST_DiagTable::offset). The BLAST_DiagTable is one of the options for remembering per-diagonal information, and is a member of the Blast_ExtendWord (BLAST_extend.h) structure.
The ungapped extension algorithm previously described is sometimes called the '1-hit wordfinder', because a single (q_off, s_off) seed is all that is required to trigger ungapped extensions. Unfortunately, protein sequences can have many seed alignments embedded inside regions that are otherwise not similar at all. By 1997 BLAST was spending 90% of its time generating ungapped alignments that did not score high enough to exceed the cutoff score.
The 2-hit wordfinder only goes to the trouble of performing an ungapped extension if two seeds wind up on the same diagonal within a certain distance of each other. This is an attempt to only perform ungapped extensions that have a high likelihood of producing a good-scoring alignment, under the assumption that most good alignments will contain many seed hits packed close together on the same diagonal. The 1997 BLAST paper estimated that use of the 2-hit algorithm tripled the speed of the wordfinder. Recent internal studies on 'well behaved' biological sequences have shown that what is rare is not just two hits close together on the same diagonal, it is actually that there are two hits on the same diagonal at all!
The 2-hit algorithm for protein sequences is implemented in the high-level function BlastAaWordFinder_TwoHit, with the actual ungapped extension performed by BlastAaExtendTwoHit. Seeds that hit to the same diagonal and whose subject offsets differ by less than window_size (the default value of window_size depends on the score matrix used; it is 40 for BLOSUM62) will trigger an ungapped extension. The modifications to the 1-hit wordfinder are relatively straightforward, but there are corner cases that need special attention.
Ungapped extension code is passed the offsets of both hits. The assumption is that the hit with the lower subject offset occurred sometime in the past, and the second hit has the larger subject offset. This is guaranteed because seeds are processed in order of increasing subject offset. Extension to the left and the right happens from the second hit. In the description below, the first seed is the 'left hit' and the second seed is the 'right hit', since that's the order in which they appear on the diagonal.
The ungapped extension proceeds as follows.
1.Determine the highest-scoring prefix of the right hit, i.e. the highest-scoring group of letters that starts at the first letter of the hit
2.Starting from the first letter before the right hit, perform a left extension identical to that of the 1-hit algorithm
3.If the extension managed to reach the last letter of the left hit, then starting from the first letter after the right hit, perform a right extension identical to that of the 1-hit algorithm
Note that in the 2-hit case attempting the right extension is optional, whereas in the 1-hit wordfinder attempting it is mandatory. Step 1 therefore needs to build up the starting score as much as possible before the left extension begins, since if the left extension cannot go far enough then the right extension will not happen at all. Finally, the ungapped extension must remember whether extension to the right actually was attempted, and if so how far to the right it explored.
As with the 1-hit wordfinder, an array of DiagStruct structures tracks the maximum subject offset explored on each diagonal. As before, the last_hit field holds the subject offset of the last seed that hit on this diagonal. For the 2-hit wordfinder each DiagStruct also uses a 1-bit boolean that is set if the first of two hits to the diagonal has not been found, and is cleared if the second hit has not been found. last_hit has a bias added in, to avoid having to be reset for each subject sequence (see previous section).
The complete 2-hit algorithm is described below. The code is basically a state machine for each diagonal, with two states (first hit found / first hit not found) and some complicated conditions for transitioning between those two states. If an extension happens then the portion of the diagonal that it explored is remembered to avoid triggering future extensions; otherwise the algorithm relies on most seeds not having neighbors nearby on the same diagonal. This does mean that the 2-hit algorithm will miss some alignments that the 1-hit algorithm will find. To compensate for this reduced sensitivity, use of the 2-hit algorithm is accompanied by a slightly lower threshold for putting query offsets into the lookup table. This has the effect of increasing the number of seeds to deal with; the time that the 2-hit wordfinder saves in ungapped alignments avoided far outweighs the extra time spent throwing away an increased number of seed hits.
Some notes on this implementation:
-
obviously this is much more complicated than the 1997 BLAST paper suggests, and is much more complex than the 1-hit wordfinder
-
the old engine implementation of this algorithm is very different. Diag structures there have two words instead of one, and this lets the old engine find a small number of hits that this code does not find. The reason is that in rare cases, the old engine code allows an ungapped alignment to start when it mostly overlaps a previously found ungapped alignment. Having one diagonal offset instead of two does not provide enough information for the current implementation to mimic that behavior. Our tests have not shown any gapped alignments that have been missed as a result of this
-
all of the booleans begin with arbitrary values when the first seeds arrive. This is okay; as long as (
s_off+ bias) always exceedslast_hit, the state machine initializes properly independent of the starting boolean value
Finally, the procedure for initializing and updating the diag array for a new subject sequence needs to change for the 2-hit wordfinder. Previously, the bias added to diag entries gets incremented by the length of the subject sequence, and when clearing the diag array (once per gigabyte of subject sequences) all the last_hit fields just need to be set to zero. The first item guarantees that diag entries get replaced when they are no longer valid. Both items together guarantee the first hit on a diagonal by seeds from a new subject sequence is automatically saved.
For the 2-hit wordfinder, last_hit does not get updated unless a hit is further down the diagonal than window_size from the previous hit. Therefore, if there is no previous hit then last_hit must be initialized to -window_size to guarantee that the first hit to a diagonal is automatically saved. If last_hit started as zero, then hits whose subject offset is between 0 and window_size-1 would never be saved, meaning that alignments may be erroneously skipped if they are near the beginning of the subject sequence. Similarly, the bias should start as window_size, so that it is (subject_length+window_size) when moving to the next subject sequence. Otherwise, if a previous hit has a subject offset near the end of the subject sequence and the next subject sequence hits that diag with an offset between 0 and window_size-1, last_hit will not get replaced like it should (i.e. stale information will remain in the diag entry). A single routine (Blast_ExtendWordExit) handles updating both wordfinders, since the 1-hit wordfinder is defined to have a window_size of zero.
for (each seed) {
q_off = query offset of seed
s_off = subject offset of seed
diag = entry of diag array describing the diagonal on which the seed lies
if (diag->flag == true) {
/* first hit not found */
if (s_off + bias < diag->last_hit) {
/* a previous extension has already explored the neighborhood
of the diagonal containing s_off; do nothing */
} else {
diag->last_hit = s_off + bias /* first hit found */
diag->flag = false;
}
} else {
/* this could be the second hit */
last_hit_d = s_off - diag->last_hit /* distance to last seed on diag */
if (last_hit_d > window) {
/* the distance to the last hit is too large; current
hit becomes last hit without perfoming extension */
diag->last_hit = s_off + bias
continue;
}
if (last_hit_d < word_size) {
/* current hit and first hit overlap; do nothing */
continue;
}
/* current hit is inside the window; trigger an extension */
perform ungapped extension from (q_off, s_off)
if (alignment score >= cutoff_score) {
/* save the alignment */
}
if (extension to right happened) {
/* a big chunk of the diagonal was explored. Start looking
for future first hits, and ignore seeds that do not extend
at least one letter beyond the neighborhood already explored */
diag->last_hit = max_right_extend - (word_size - 1) + bias
diag->flag = true
} else {
diag->last_hit = s_off + bias /* last hit = current hit */
}
}
}
For all versions of nucleotide BLAST, the function responsible for converting seed hits into ungapped alignments is BlastNaWordFinder (na_ungapped.c). Many of the principles are the same compared to the protein wordfinder, but there are changes necessary because the sequences involved can be very large, the word size can be different from the number of letters indexed in the lookup table, and the subject sequence is always in compressed form.
All of the different nucleotide routines rely on the same ungapped extension, performed by s_NuclUngappedExtendExact. It has a few differences from the protein ungapped extension algorithm:
-
the subject sequence is assumed to be in compressed form, so that its letters must be extracted one at a time
-
extension to the left begins one letter before the seed hit, but extension to the right begins at the first letter of the seed. Both extensions only use the X-drop test.
There is no shortcut for right extensions like protein ungapped code uses. This is mainly historical, but sometimes (i.e. in discontiguous megablast) the initial seed can contain mismatches, and so will have a low starting score that would make the extension risk terminating prematurely unless the full X-drop criterion was applied. For X values that are reasonable we can expect to at least achieve the highest-scoring prefix to the seed. Another reason to explore the seed itself during the right extension is that s_NuclUngappedExtendExact actually uses a nucleotide score matrix (rather than registering only matches and mismatches), and this is the first time that actual scores, that include ambiguities in the query sequence, are calculated for the alignment.
For blastn with default parameters, ungapped extensions do not take much of the total time. However, when the word size is small the time needed for ungapped extensions is a critical bottleneck. Such small searches involve far more seeds extracted from the lookup table, and the small size of these words means an extension is more likely to be triggered.
When ungapped nucleotide extensions are a bottleneck, the vast majority of them do not achieve a high-enough score to be saved. This suggests that an approximate ungapped extension that is faster could be used by default.If the approximate score achieved exceeds a more generous cutoff value then the full ungapped extension is computed.
The exact left extension schematically works as follows (the right extension is similar):
sum = 0;
while (letters left in both sequences) {
subject_off -= 1
query_off -= 1
extract base 'subject_off' from the byte of the
compressed subject sequence containing it
sum += matrix[q_base][s_base]
if (sum > 0) {
mark new alignment start point
score += sum
sum = 0;
} else if (sum < X) {
break;
}
}
Note the multiple pointer decrements, use of a score matrix, and the pair of branches (the first of which is unpredictable) that happen for each letter in the extension. Reducing the time needed to compute the extension should involve removing as many of these operations as possible. Some simplifications can help:
-
The approximate extension should only count matches and mismatches. This will overestimate the penalty associated with ambiguities, but allows precomputations that save time
-
The extension may only start and end on a 4-base boundary of the subject sequence
These two simplifications allow an effective unrolling by four of the inner loop: one table lookup, one pair of comparisons, and one pair of base extractions for every four positions of the query and subject. The table lookup at iteration i really only needs to determine the score for the ith group of four letter-letter alignments, which in turn only depends on how many of those 4 are matches and how many are mismatches. We can precompute this information with an 8-bit hashtable.
For example:
| Label | Value |
|---|---|
| Query: | A A C G |
| in binary: | 00 00 01 10 |
| Subject: | A C C A |
| in binary: | 00 01 01 00 |
| Query XOR Subject |
00 01 00 10 (index into hashtable) |
In the example above, the table will contain the score for two matches and two mismatches at index 00010010. Since matches are interchangeable with each other and mismatches are similarly interchangeable, the modified extension code looks like:
sum = 0;
while (groups of 4 bases left in both sequences) {
subject_off -= 4
query_off -= 4
pack next 4 query bases into q_byte
sum += table[q_byte XOR s_byte]
if (sum > 0) {
mark new alignment start point
score += sum
sum = 0;
} else if (sum < X) {
break
}
}
Especially when the match and mismatch penalties are close to each other in magnitude, the above will be much faster (up to four times faster) than the original extension.
What must the cutoff for the approximate extension be? It must be smaller than the ordinary ungapped cutoff, but making it too small will cause the exact ungapped alignment to run too often. Empirically, setting it to floor(60% of the ungapped cutoff) is a reasonable compromise: the vast majority of exact ungapped extensions are avoided, and I have yet to see an ungapped alignment that is missed. It's possible that the cutoff should instead be represented as the ordinary cutoff plus the score for a few mismatches, since most of the time the approximate ungapped alignment will look like the exact alignment with some spurious letters to either side. However, when the ordinary cutoff is somewhat small both these schemes lead to approximate cutoffs that are about the same.
The table for approximate ungapped extension is computed in BlastInitialWordParametersNew, and the extension itself happens in s_NuclUngappedExtend. This is the only entry point for nucleotide ungapped extensions.
For blastn with default parameters the runtime difference is essentially zero; however, as the word size goes down and the match/mismatch penalties converge to each other, the speedup is significant (30-50%). One side effect of using approximate extensions is that the generated alignment will not extend to the right as far as it used to on average, which limits the amount of pruning of future seed alignments that is possible. Hence the number of ungapped extensions performed increases slightly (~5-8%), but the slowdown from this is more than offset by the speedup from the extensions themselves being faster.
The complexity in the nucleotide wordfinders actually has more to do with the seeds returned from the lookup tables, or equivalently deciding when to call s_NuclUngappedExtend and whether preprocessing of the seed must happen first. BlastNaWordFinder runs the previously determined ScanSubjectroutine on the subject sequence as many times as is needed to scan the whole subject. For each of the seed hits returned (they come in batches), we must determine if the seed belongs to a run of exact matches equal to at least the BLAST wordsize in length. The routine that does that varies from search to search, and is chosen by BlastChooseNaExtend(na_ungapped.c) when the search begins, using information from the lookup table. The choice of 'exact match extension' routine is stored as an opaque pointer within the lookup table structure.
The extension process here is not very elaborate; the objective is to determine as quickly as possible if a seed alignment lies in a field of sufficiently many exact matches. Performance is more important here than with the complete ungapped extension, since if the lookup table width does not match the BLAST word size then every single seed alignment must undergo this exact match extension.
There are several exact match extension functions to choose from (all are in na_ungapped.c):
-
s_BlastNaExtendDirectperforms no exact match extension at all, and merely forwards every seed to the ordinary ungapped extension routines. This is used when the lookup table width matches the word size, and applies to any lookup table type -
s_BlastNaExtendis a generic routine that performs exact match extensions assuming the lookup table is of typeBlastNaLookupTableorBlastMBLookupTable -
s_BlastNaExtendAlignedworks likes_BlastNaExtend, except that it assumes the number of bases in a lookup table word, and the start offset of each hit, is a multiple of 4 -
s_BlastSmallNaExtendperforms the exact match extension process assuming the lookup table is of typeBlastSmallNaLookupTable. This routine and the next use special precomputations that make them much faster than their counterparts above -
s_BlastSmallNaExtendAlignedOneByteworks likes_BlastSmallNaExtend, but assumes the number of bases in a lookup table word and the start offset of each hit is a multiple of 4, and also that the word size is within 4 bases of the lookup table width. This allows the routine to omit loop and function overhead that the previous routine requires, and makes it the fastest of all the routines that perform exact match extensions. Happily, in practice this routine is what blastn with default parameters will use for the vast majority of searches
The exact match extension first occurs to the left of the seed and stops at the first mismatch between the query and subject sequences. Ambiguities in the query sequence are always treated as mismatches. When the left extension is complete, if more exact matches are needed to achieve the blastn word size then a right extension is performed, starting from the end of the seed. The seed itself is always assumed to contain only exact matches. While this is not true for discontiguous megablast, in that case the lookup table width matches the word size of the search, so that exact match extensions are not necessary at all.
Because the subject sequence is compressed, it is technically possible to compare letters in batches of four when performing these extensions to the left and right, then on the first mismatch to go back and compare one letter at a time. However, this will slow down the common case: since the nucleotide alphabet has four letters, the first letter pair beyond the seed will be a mismatch 3/4 of the time (assuming the sequences are random). Thus most of the time an extension will encounter a mismatch very quickly, and the speed can be improved if we always compare one letter at a time since this has much less overhead. Concentrating on reduction of overhead rather than processing letters in parallel makes the exact match phase run more than twice as fast on average. Especially for searches with small word size, where it is customary to find a huge number of seeds, fast exact match extensions are essential.
Most queries are small, and if exact match extensions proceed one base at a time, then the previous routines would still require several loop iterations to complete the exact match extension. Typically the BLAST word size is 11 and the lookup table has width 8, so that 2-3 letters must be tested. If the subject sequence was compressed by four, then 1-2 table lookups would be sufficient to complete the extension, and would be much faster. This doesn't invalidate the conclusions of the previous section: compressing the query sequence on the fly adds unacceptable overhead, but if the query was compressed once, at the beginning of the search, then using table lookups to determine the number of additional exact matches removes setup and loop overhead, allowing a net savings. When the lookup table is of type BlastSmallNaLookupTable, we can be assured that the query is small, so it's feasible to compress the query.
The SmallNa exact match extension routines take advantage of this preprocessing (first published by Cameron and Williams). When the query is first created, a call to BlastCompressBlastnaSequence compresses it 4-to-1. The compressed array has one byte for every query position, plus three extra bytes at the beginning. The compressed array is set up so that offset i of the array gives the packed representation of bases i to i+3, and iterating through the query amounts to iterating through the compressed array with stride 4. This fourfold redundancy means that all groups of 4 bases within the query are aligned on a byte boundary, so that a seed hit can start at any query offset and pull groups of 4 bases from the compressed array without having to realign them. The handling of bases at the start or end of the query is special; for query length L, the compressed array is of length C = _L + _3, and the start of the array is a pointer to offset 3 of C.
- offset -3 gives the first base, right-justified in a byte
- offset -2 gives the first 2 bases, right-justified in a byte
- offset -1 gives the first 3 bases, right-justified in a byte
- offset i, 0 <= i < C - 4, of the compressed array gives the 4 bases starting at offset i of the query, packed together
- offset C - 3 gives the last 3 bases, left-justified in a byte
- offset C - 2 gives the last 2 bases, left-justified in a byte
- offset C - 1 gives the last base, left-justified in a byte
Queries of length less than 4 bases have the same representation, except that nonexistent bases have a value of 0 in the first three compressed entries, and are not represented at all in the last entries of the compressed array.
With the compressed array in place, we need two 256-entry tables, for extensions to the left and right. Entry i of the left extension table contains floor(number of trailing zero bits in the binary representation of i) / 2 and entry i of the right extension table does the same but with leading zero bits. With these precomputed quantites, the number of exact matches to the left of a seed hit at offset (q,s) on the query and subject sequences is
min(q, s, bases_allowed,
left_table[compressed_query[q-4] XOR subject[s-1]] )
assuming q and s are positive (note that the format of the compressed query puts valid data at offset q-4 when this is negative). A similar but more tedious 4-term min applies to the right extension, if it turns out to be necessary. The streamlined extension process allows an overall speedup approaching 15% for blastn with default parameters and a small query.
s_BlastSmallNaExtend reuses the compressed query to perform arbitrary-size exact match extensions. Unfortunately, this is only slightly faster than the base-at-a-time implementation, for reasons detailed in the previous section, and also because the extension process cannot skip over the entire seed (bytes of the subject sequence must remain aligned). One future item to do is to allow use of the compressed query for the full ungapped extension. This can provide a big speedup for blastn with a small query and word size 7, which is somewhat popular and where 30% of the time is spent performing ungapped extensions.
Whether or not a seed is extended out to the full word size expected, at some point an attempt may be made to extend that seed into a true ungapped alignment that may contain mismatches and uses a conventional X-drop algorithm. There are two routines that perform this function, s_BlastnDiagHashExtendInitialHit and s_BlastnDiagExtendInitialHit (in na_ungapped.c). Each calls s_NuclUngappedExtend as necessary.
Like their protein sequence counterparts, the nucleotide wordfinders use auxiliary data structures to throw away seeds that will just repeat the work of previous ungapped alignments. s_BlastnDiagExtendInitialHit use an array of DiagStruct structures to track the furthest extent of the last hit on each diagonal. Each DiagStruct has a 31-bit field for the last offset on that diagonal and a 1-bit boolean that defines what the 31-bit field means. If the top bit in a DiagStruct is set, it means that the lower 31 bits is the offset of the first hit (out of 2 that the 2-hit algorithm would need). If the top bit is clear then the lower 31 bits give the maximum extent of ungapped alignments on that diagonal, which helps in removing seed hits that occur in regions of the diagonal that have already been explored. The data structures needed for this are stored in a BLAST_DiagTable.
Even with only four bytes per diagonal, a diag array can consume excessive amounts of memory when the query is large. Further, if long alignments with high identity are expected then it is typical to get long runs of seeds that hit to the same diagonal. This implies that even with a full diag array available, only a few of the entries would ever be used at a given time. Under these circumstances we can save the memory of a diag array at the expense of a small increase in runtime by using a hashtable of diag entries rather than a random-access data structure. s_BlastnDiagHashExtendInitialHit implements this improvement.
The hashtable is implemented as an array of DIAGHASH_NUM_BUCKET(=512) integers, acting as a front end for an array of initially DIAGHASH_CHAIN_LENGTH (=256) DiagHashCell structures. These basically wrap an ordinary DiagStruct along with a next pointer and a word to tell which diagonal the struct is for. Each hash bucket stores the offset of a linked list of diagonals that hash to that bucket, and all the linked lists are packed together in the 'chain' field of a BLAST_DiagHash struct. This behavior is very similar to the way the megablast lookup table works.
Processing happens one seed at a time; for each seed, whether extended to the full word size or not, the hashtable entry that contains the corresponding diagonal is first located in s_BlastDiagHashRetrieve. If the entry is not found, a new entry is added to the list for that has bucket. If the entry is found, the 1-hit or 2-hit algorithm proceeds using that entry. This layout makes it easy to increase the number of diagonals stored. A final optimization is that like the protein wordfinder, the hashtable does not have to be cleared when switching from one database sequence to the next. Both the diag array and the hashtable implementations maintain a bias (the 'offset' field in those structures) that is added to the computed values of diagonal distance, and the bias can be used to tell when a diagonal has 'gone stale' and its corresponding diag struct can be recycled for use by another diagonal.
A final wrinkle in the use of ungapped extensions is that all of them are optional. In particular, discontiguous megablast is configured by default to skip ungapped extensions entirely, so that all of the diag machinery works but seeds that survive are simply saved in a BlastInitHSP structure directly. Discontiguous megablast in this configuration forwards lookup table hits directly to the subsystem for gapped extensions. This effectively turns off all of the diag machinery used for ungapped extensions, since lookup table hits will only be pruned if they lie a distance larger than (scanning stride) away from previous lookup table hits on the same diagonal. When there are clusters of seeds this still can amount to a lot of pruning, although this process only works well with 2-hit extensions, to reduce the number of seeds that are forwarded.